CTFcrypto

First Post:

Last Update:

Word Count:
11.8k

Read Time:
59 min

Page View: loading...

栅栏密码

栅栏密码把要加密的明文分成 N 个一组，然后把每组的第 1 个字连起来，形成一段无规律的话。

1
明文：THERE IS A CIPHER

去掉空格后变为

1
THEREISACIPHER

分成两栏，两个一组得到

1
TH ER EI SA CI PH ER

先取出第一个字母，再取出第二个字母

1
2
TEESCPE
HRIAIHR

连在一起就是

1
TEESCPEHRIAIHR

上述明文也可以分为 2 栏。

1
THEREIS ACIPHER

组合得到密文

1
TAHCEIRPEHIESR

摩斯密码

培根密码

培根密码使用两种不同的字体，代表 A 和 B，结合加密表进行加解密。

a AAAAA g AABBA n ABBAA t BAABA
b AAAAB h AABBB o ABBAB u-v BAABB
c AAABA i-j ABAAA p ABBBA w BABAA
d AAABB k ABAAB q ABBBB x BABAB
e AABAA l ABABA r BAAAA y BABBA
f AABAB m ABABB s BAAAB z BABBB

上面的是常用的加密表。还有另外的一种加密表，可认为是将 26 个字母从 0 到 25 排序，以二进制表示，A 代表 0，B 代表 1。

下面这一段内容就是明文 steganography 加密后的内容，正常字体是 A，粗体是 B：

To encode a message each letter of the plaintext is replaced by a group of five of the letters ‘A’ or ‘B’.

可以看到，培根密码主要有以下特点

  • 只有两种字符
  • 每一段的长度为 5
  • 加密内容会有特殊的字体之分，亦或者大小写之分。

Base 编码

base xx 中的 xx 表示的是采用多少个字符进行编码，比如说 base64 就是采用以下 64 个字符编码，由于 2 的 6 次方等于 64，所以每 6 个比特为一个单元，对应某个可打印字符。3 个字节就有 24 个比特，对应于 4 个 Base64 单元，即 3 个字节需要用 4 个可打印字符来表示。它可用来作为电子邮件的传输编码。在 Base64 中的可打印字符包括字母 A-Z、a-z、数字 0-9，这样共有 62 个字符，此外两个可打印符号在不同的系统中而不同。

JSfuck

JSFuck 是一种基于 JavaScript 原子部分的深奥和教育性的编程风格。它仅使用六个不同的字符来编写和执行代码。

它不依赖于浏览器，因此您甚至可以在 Node.js 上运行它。

基本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
false       =>  ![]
true        =>  !![]
undefined   =>  [][[]]
NaN         =>  +[![]]
0           =>  +[]
1           =>  +!+[]
2           =>  !+[]+!+[]
10          =>  +[[+!+[]]+[+[]]]
Array       =>  []
Number      =>  +[]
String      =>  []+[]
Boolean     =>  ![]
Function    =>  []["filter"]
run         =>  []["filter"]["constructor"](CODE)()
eval        =>  []["filter"]["constructor"]("return eval")()( CODE)
window      =>  []["filter"]["constructor"]("return this")()

完整列表：jsfuck/jsfuck.js at master · aemkei/jsfuck · GitHub

可在浏览器控制台运行。

AAEncode

http://www.atoolbox.net/Tool.php?Id=703

Rabbit

image-20220520141358420

http://www.jsons.cn/rabbitencrypt/

Ook 编码

[Brainfuck/Ook! Obfuscation/Encoding splitbrain.org]

Brainfuck 解释器

[Brainfuck/Ook! Obfuscation/Encoding splitbrain.org]

Serpent 加密

http://serpent.online-domain-tools.com/

可以用 ARCHPR 暴力破解压缩包

Quoted-printable 编码

一堆等号连接的 16 进制数对 -Quoted-printable 编码

http://web.chacuo.net/charsetquotedprintable

MD5 碰撞

https://www.somd5.com/

MD5 是什么

MD5 信息摘要算法（英语：MD5 Message-Digest Algorithm），一种被广泛使用的密码散列函数，可以产生出一个 128 位（16[字节] 的散列值（hash value）），用于确保信息传输完整一致。MD5 由美国密码学家 [罗纳德·李维斯特]（Ronald Linn Rivest）设计，于 1992 年公开，用以取代[MD4] 算法。这套算法的程序在 RFC 1321 标准中被加以规范。1996 年后该算法被证实存在弱点，可以被加以破解，对于需要高度安全性的数据，专家一般建议改用其他算法，如 [SHA-2]。2004 年，证实 MD5 算法无法防止碰撞，因此不适用于安全性认证，如[SSL] 公开密钥认证或是 [数字签名] 等用途。

MD5 碰撞原理简单介绍及其实现 - wysng - 博客园 (cnblogs.com)

URL 解码

http://www.urlencode.com.cn/

RSA

RSA 算法

密钥生成的步骤

我们通过一个例子，来理解 RSA 算法。假设爱丽丝要与鲍勃进行加密通信，她该怎么生成公钥和私钥呢？

第一步，随机选择两个不相等的质数 p 和 q。

爱丽丝选择了 61 和 53。（实际应用中，这两个质数越大，就越难破解。）

第二步，计算 p 和 q 的乘积 n。

爱丽丝就把 61 和 53 相乘。

n = 61×53 = 3233

n 的长度就是密钥长度。3233 写成二进制是 110010100001，一共有 12 位，所以这个密钥就是 12 位。实际应用中，RSA 密钥一般是 1024 位，重要场合则为 2048 位。

第三步，计算 n 的欧拉函数φ(n)。

n 是质数，则 φ(n)=n-1
n = p1 × p2
φ(n) = φ(p1p2) = φ(p1)φ(p2)
=> φ(n) = (p-1)(q-1)

爱丽丝算出φ(3233)等于 60×52，即 3120。

第四步，随机选择一个整数 e，条件是 1< e < φ(n)，且 e 与φ(n) 互质。

爱丽丝就在 1 到 3120 之间，随机选择了 17。（实际应用中，常常选择 65537。）

第五步，计算 e 对于φ(n)的模反元素 d。

所谓”模反元素”就是指有一个整数 d，可以使得 ed 被φ(n)除的余数为 1。

ed ≡ 1 (mod φ(n))

这个式子等价于

ed - 1 = kφ(n)

于是，找到模反元素 d，实质上就是对下面这个二元一次方程求解。(-k = y)

ex + φ(n)y = 1

已知 e=17, φ(n)=3120，

17x + 3120y = 1

这个方程可以用 “扩展欧几里得算法”(又叫辗转相除法) 求解，此处省略具体过程。总之，爱丽丝算出一组整数解为 (x,y)=(2753,-15)，即 d=2753。

至此所有计算完成。

第六步，将 n 和 e 封装成公钥，n 和 d 封装成私钥。

在爱丽丝的例子中，n=3233，e=17，d=2753，所以公钥就是 (3233,17)，私钥就是（3233, 2753）。

实际应用中，公钥和私钥的数据都采用 ASN.1 格式表达。

RSA 算法的加密和解密

有了公钥和密钥，就能进行加密和解密了。

(1)加密要用公钥(n,e)

假设鲍勃要向爱丽丝发送加密信息 m，他就要用爱丽丝的公钥 (n,e) 对 m 进行加密。这里需要注意，m 必须是整数（字符串可以取 ascii 值或 unicode 值），且 m 必须小于 n。

所谓”加密”，就是算出下式的 c：

　me ≡ c (mod n)

爱丽丝的公钥是 (3233, 17)，鲍勃的 m 假设是 65，那么可以算出下面的等式：

65^17 ≡ 2790 (mod 3233)

于是，c 等于 2790，鲍勃就把 2790 发给了爱丽丝。

(2)解密要用私钥(n,d)

爱丽丝拿到鲍勃发来的 2790 以后，就用自己的私钥(3233, 2753) 进行解密。可以证明，下面的等式一定成立：

cd ≡ m (mod n)

也就是说，c 的 d 次方除以 n 的余数为 m。现在，c 等于 2790，私钥是(3233, 2753)，那么，爱丽丝算出

2790^2753 ≡ 65 (mod 3233)

因此，爱丽丝知道了鲍勃加密前的原文就是 65。

至此，”加密–解密”的整个过程全部完成。

我们可以看到，如果不知道 d，就没有办法从 c 求出 m。而前面已经说过，要知道 d 就必须分解 n，这是极难做到的，所以 RSA 算法保证了通信安全。

你可能会问，公钥(n,e) 只能加密小于 n 的整数 m，那么如果要加密大于 n 的整数，该怎么办？有两种解决方法：一种是把长信息分割成若干段短消息，每段分别加密；另一种是先选择一种”对称性加密算法”（比如DES），用这种算法的密钥加密信息，再用 RSA 公钥加密 DES 密钥。

(71 条消息) RSA 加密算法_gao131360144 的博客 -CSDN 博客_rsa 加密算法

依赖库：

  • gmpy2
  • pycrypto

RSA 原理

私钥 n,d，公钥 n,e。其中 n 是两个素数 p,q 的乘积。c 为密文，m 为明文。φ(n)为欧拉函数。其中:d 是 e 模φ(n)的逆元。我们有φ(n)=(p−1)(q−1)

ed≡1modφ(n)

encrypt:c≡memodn

decrypt:m≡cdmodn

openssl 使用

使用 openssl 查看 pem 文件：

1
openssl rsa -pubin -text -modulus -in public.pem

使用 openssl 和私钥解密

1
openssl rsautl -decrypt -in flag -inkey privatekey -out flag.txt

常规

场景

已知 p、q、c

解法

求φ(n)，再求出 d 即可

1
2
3
4
5
6
7
8
9
10
from Crypto.Util.number import inverse,long_to_bytes
p = 
q = 
n = p*q
phi = (p-1)*(q-1)
e = 
d = inverse(e,phi)
c = 
m = pow(c,d,n)
print(long_to_bytes(m))

模不互素

场景

已知如下：

n1=p×q1

n2=p×q2

c1=memodn1

c2=memodn2

解法

求出 n1 和 n2 的公因子，即可解得 p 和 q

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from libnum import xgcd
from Crypto.Util.number import inverse,long_to_bytes
n1 = 
n2 = 
c1 = 
c2 = 
e = 
p = xgcd(n1,n2)[2]
q1 = n1//p
q2 = n2//p
phi1=(p-1)*(q1-1)
phi2=(p-1)*(q2-1)
d1 = inverse(e,phi1)
d2 = inverse(e,phi2)
m1 = pow(c1,d1,n1)
m2 = pow(c2,d2,n2)
print(long_to_bytes(m1))
print(long_to_bytes(m2))

共模攻击

场景

模数 n 相同，指数、e1、e2 不同且互质

已知：

c1=me1modn

c2=me2modn

解法

根据扩展欧几里得算法求出 re1+se2=1modn 的整数、r、s

根据
(1)c1rc2s≡mre1mse2modn≡mmodn 得到明文

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from libnum import xgcd
from Crypto.Util.number import inverse,long_to_bytes

n = 
c1 = 
c2 = 
e1 = 
e2 = 
s = xgcd(e1,e2)
s1 = s[0]
s2 = s[1]
if s1 < 0:
    s1 = - s1
    c1 = inverse(c1, n)
elif s2 < 0:
    s2 = - s2
    c2 = inverse(c2, n)

m = pow(c1, s1, n)*pow(c2, s2, n) % n print(long_to_bytes(m))

e 小指数攻击

场景

当 e 很小的时候，例如 2、3，此时可能可以通过直接暴力开根的方式进行攻击

解法

以 e=3 为例，已知 c≡m3modn，因此有：m3=c+kN

m=c+kN3

1
2
3
4
5
6
7
8
9
10
11
import gmpy2
from Crypto.Util.number import long_to_bytes
n = 
e = 3
c = 
i = 0
while(True):
    a,b = gmpy2.iroot(c+i*n,3)
    if(b==1):
        print(long_to_bytes(a))
        exit(0)

Rabin 攻击

场景

当指数 e=2，且已知 p 和 q

解法

  • 计算

    mp=c2modp

    mq=c2modq

  • 扩展欧几里得求 yp 和 yq

    ypp+yqq=1

  • 解得 4 个明文

    a=(yp⋅p⋅mq+yq⋅q⋅mp)modn

    b=n−a

    c=(yp⋅p⋅mq−yq⋅q⋅mp)modn

    d=n−c

  • 条件：当 p≡q≡3mod4 时，有

    mp=c(p+1)/4modp

    mq=c(q+1)/4modq

满足条件时

1
2
3
4
5
6
7
8
9
10
11
12
import gmpy2
def rabin_decrypt(c, p, q, e=2):
    n = p * q
    mp = pow(c, (p + 1) / 4, p)
    mq = pow(c, (q + 1) / 4, q)
    yp = gmpy2.invert(p, q)
    yq = gmpy2.invert(q, p)
    r = (yp * p * mq + yq * q * mp) % n
    rr = n - r
    s = (yp * p * mq - yq * q * mp) % n
    ss = n - s
    return (r, rr, s, ss)

不满足条件时

转换为模平方根问题

  • 用 python（代码来自 yuri）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
import gmpy2
import random

def exgcd(r0, r1):
    x0, y0 = 1, 0
    x1, y1 = 0, 1
    x, y = r0, r1
    r = r0 % r1
    q = r0 // r1
    while r:
        x, y = x0 - q * x1, y0 - q * y1
        x0, y0 = x1, y1
        x1, y1 = x, y
        r0 = r1
        r1 = r
        r = r0 % r1
        q = r0 // r1
    return x

def Jacobi(n, m):
    n = n % m
    if n == 0:
        return 0
    Jacobi2 = 1
    if not (n & 1):
        k = (-1) ** (((m**2 - 1) // 8) & 1)
        while not (n & 1):
            Jacobi2 *= k
            n >>= 1
    if n == 1:
        return Jacobi2
    return Jacobi2 * ((-1) ** ((((m - 1) // 2) * ((n - 1) // 2)) & 1)) * Jacobi(m % n, n)

def CRT(b, m): 
    M = 1
    for i in range(len(b)):
        M *= m[i]
    ans = 0
    for i in range(len(b)):
        ans += b[i] * M // m[i] * exgcd(M // m[i], m[i])
    return ans % M

def solve(a, p):
    a_1 = gmpy2.invert(a, p)
    s = p - 1
    t = 0
    while s % 2 == 0:
        t += 1
        s >>= 1
    n = 0
    while True:
        n = random.randint(1, p-1)
        if Jacobi(n, p) == -1:
            break

    b = pow(n, s, p)
    x_t_1 = pow(a, (s+1)//2, p)

    assert pow(b, 2**t, p) == 1
    assert pow(b, 2**(t-1), p) == p-1

    x, j, temp = 0, 0, 0

    for i in range(0, t-1):
        x = pow(a_1*(x_t_1**2), 2**(t-2), p)
        if x == 1:
            j = 0
        elif x == p-1:
            j = 1
        else:
            exit(0)
        t -= 1
        temp = x_t_1
        x_t_1 = (x_t_1 * (b**(j**(2**i)))) % p
    else: 
        if x == 1:
            return temp, -temp % p


p = 
q = 
n = p * q
e = 2
c = 

a, b = None, None
while True:
    try:
        a = solve(c % p, p)
        assert pow(a[0], e, p) == c % p
        assert pow(a[1], e, p) == c % p
        break
    except:
        pass

while True:
    try:
        b = solve(c % q, q)
        assert pow(b[0], e, q) == c % q
        assert pow(b[1], e, q) == c % q
        break
    except:
        pass

print(bytes.fromhex(hex(CRT([a[0],b[0]],[p,q]))[2:]))
print(bytes.fromhex(hex(CRT([a[0],b[1]],[p,q]))[2:]))
print(bytes.fromhex(hex(CRT([a[1],b[0]],[p,q]))[2:]))
  • 用 sage

使用一句话 Mod(c_square, q).sqrt(all=True) 分别求出 mp 和 mq，代回去解得可能的明文

n 分解攻击

当 n 很小或者满足一定条件时，可以进行暴力分解

  • yafu
  • factordb
  • 当 d<1/3N1/4 时，通过 Wiener’s attack 能够攻击得到 d
  • 当、p、q 十分接近时，可以使用费马分解分解 n
  • 当 q 较小，即 |p−q| 较大时，可以爆破 q
  • 当 d<N0.292 时，通过 Boneh Durfee Method 分解 n

广播攻击

场景

给定了不同的模数 ni，但指数 e 相同

已知:

c1=memodn1

c2=memodn2

c3=memodn3

解法

使用中国剩余定理进行广播攻击

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from gmpy2 import *
from Crypto.Util.number import long_to_bytes
def broadcast(n1, n2 ,n3, c1, c2, c3):
    n = [n1, n2, n3]
    C = [c1, c2, c3]
    N = 1
    for i in n:
        N *= i

    Ni = []
    for i in n:
        Ni.append(N / i)

    T = []
    for i in range(3):
        T.append(long(invert(Ni[i], n[i])))

    X = 0
    for i in range(3):
        X += C[i] * Ni[i] * T[i]

    m = X % N
    return m

n1 = 
n2 = 
n3 = 
e = 
c1 = 
c2 = 
c3 = 
result = broadcast(n1,n2,n3,c1,c2,c3)
m = iroot(result, e)
print(long_to_bytes(result))

第二部分主要是一些 Oracle 相关的内容

依赖库：

  • gmpy2
  • pycrypto
  • pwntools
  • sage

选择密文攻击

场景

假设 Alice 创建密文 C=Pemodn，并发送给 Bob，并且我们有一次选择密文进行解密的机会，此时我们可以拦截 C，并通过选择密文攻击，求出 P

解法

  1. 选择任意一个 G(n)内与 n 互素的 X(一般就是 2 啦)
  2. 计算 Y=C×Xemodn
  3. 由于选择密文攻击，将 Y 作为密文我们可以得到 Z=Ydmodn
  4. 最后由于
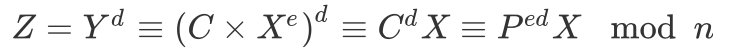
    image-20200711200846750
    可以通过逆元求出 P
1
2
3
4
5
6
7
8
9
10
11
12
13
from pwn import *
from gmpy2 import invert
from Crypto.Util.number import long_to_bytes
p = remote(ip,port)
C = 
n = 
e = 
X = 2
X_e = pow（X,e,n)
p.sendline(str((X_e*c)%n)
Z = int(p.recvline())
result = (Z*long(invert(X,n)))%n
print(long_to_bytes(result))

parity oracle

场景

假设存在一个 Oracle，它会对一个给定的密文进行解密，并且会检查解密的明文的奇偶性，并根据奇偶性返回相应的值，比如 1 表示奇数，0 表示偶数。那么给定一个加密后的密文，我们只需要 log(N) 次就可以知道这个密文对应的明文消息

解法

假设 C=PemodN

第一次我们发送 C×2e=(2P)emodN 给服务器，服务器会返回 2PmodN

我们知道：

  • 2P 是偶数，因此(2P)e 也是偶数
  • N 是奇数（不考虑存在因子为 2 时）

那么：

  • 服务器返回奇数时，说明 2P>N，且减去了奇数个 N 同时我们又知道 P<N，即 N/2≤P<N
  • 服务器返回偶数时，说明 0≤P<N/2

归纳：

假设第 i 次时，我们有

xN/2i≤P<(x+1)N/2i

在第 i+1 次时，我们可以得到

2i+1PmodN=2i+1P−kN

0≤2i+1P−kN<N

kN/2i+1≤P<(k+1)N/2i+1

根据第 i 次结果我们分子分母同乘 2，有

2xN/2i+1≤P<2(x+1)N/2i+1

那么：

  • 服务器返回奇数，则 k 必然是一个奇数，k=2y+1， 那么 (2yN+N)/2i+1≤P<(2yN+2N)/2i+1。与此同时，由于 P 必然存在，所以第 i+1 得到的这个范围和第 i 次得到的范围必然存在交集。所以 y 必然与 x 相等。
  • 服务器返回偶数，则 k 必然是一个偶数，k=2y，此时 y 必然也与 x 相等，那么 2xN/2i+1≤P<(2xN+N)/2i+1

总结：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
lb = 0
ub = N
if server returns 1
    lb = (lb+ub)/2
else:
    ub = (lb+ub)/2
from pwn import *
import time,decimal,binascii
from Crypto.Util.number import long_to_bytes

p = remote(ip,port)

def oracle(c1):
    global p
    p.sendline(str(c1))
    res = int(p.recvuntil("\n").strip())
    if res == 0: return 0
    if res == 1:
        return 1
    else:
        assert (0)


def partial(c, n):
    global c_of_2
    k = n.bit_length()
    decimal.getcontext().prec = k  
    lower = decimal.Decimal(0)
    upper = decimal.Decimal(n)
    for i in range(k):
        possible_plaintext = (lower + upper) / 2
        flag = oracle(c)
        if not flag:
            upper = possible_plaintext  
        else:
            lower = possible_plaintext 
        c = (c * c_of_2) % n  
        print(i,flag,int(upper - lower))
    return int(upper) 
  
e = 
c = 
n = 
c_of_2 = pow(2,e,n)
m = partial((c * c_of_2) % n, n)
print(long_to_bytes(m))

byte oracle

场景

假设目前存在一个 Oracle，它会对一个给定的密文进行解密，并且会给出明文的最后一个字节。那么给定一个加密后的密文，我们只需要 log256n 次就可以知道这个密文对应的明文消息。

解法

是 parity oracle 的扩展，此时泄露一个 byte，因此我们将原来的发送 C×2e 改成 C×256e 即可

已知

C=PemodN

第一次我们发送

C×256e=(256P)emodN

服务器返回 256PmodN

此时有：

  • 256P 为偶数
  • N 为奇数

由于 P<N, 我们有 256PmodN=256P−kN(k<256)，并且对于不同的，k1，k2, 我们有 256P−k1n≢256P−k2nmod256

由于是模 256，所以 256P−kn≡−knmod256，因此我们首先可以枚举 0−255 情况下的最后一个字节，并得到映射表

当服务器返回最后一个字节 b，我们就可以通过映射表得到 k，即减去了 k 个 N，有 kN≤256P≤(k+1)N

归纳：

假设在第 i 次时，有

xN/256i≤P<(x+1)N/256i

当第 i+1 次时，发送 C∗256(i+1)e，服务器返回

256i+1PmodN=256i+1P−kN

0≤256i+1P−kN<N

kN/256i+1≤P<256(x+1)N/256i+1

总结：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
lb = 0
ub = N
k = mab[b]
interval = (ub-lb)/256
lb = lb + interval * k
ub = lb + interval
from pwn import *
import time
import binascii
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes
from gmpy2 import invert
p = remote(ip,port)
e =
c = 
n = 
print("e:",e)
print("c:",c)
print("n:",n)
d = {}
for k in range(0,256):
    d[(-k*n)%256] = k
print(d)
lb = 0
ub = n
for i in range(1,256):
    m = (c * pow(256,i*e,n)) %n
    p.sendline(str(m))
    b = int(p.recvline())
    k = d[b]
    interval = int((ub-lb)/256)
    lb = lb + interval * k
    ub = lb + interval
    print("ub-lb:",ub-lb)
print("lb:",lb)
print("ub:",ub)
i = lb
# 没控制好边界，所以最后暴力一段
while(i<=lb+30000):
    m = pow(i,e,n)
    if(m==c):
        print("result:",i)
        p.sendline(str(i))
        print(p.recvline())
        exit(0)
    i+=1
print("no result")

d 泄露攻击

场景

题目同时给出了 d、e 和 N

解法

我们知道 ed≡1modφ(n)，则存在 k，使得

ed−1=kφ(n)

又有∀a∈Zn∗，满足 aed−1≡1modn，令

ed−1=2st

其中，t 是一奇数，可以证明对于至少一半的∀a∈Zn∗，存在一个 i∈[1,s]，使得

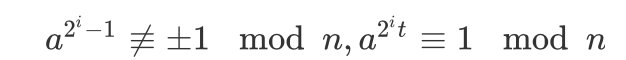
image-20200711202601842

成立，如果 a,i 满足上述条件，可以对 n 进行暴力分解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import fractions,random

def factor_modulus(n, d, e):
    """
    Efficiently recover non-trivial factors of n
    See: Handbook of Applied Cryptography
    8.2.2 Security of RSA -> (i) Relation to factoring (p.287)
    http://www.cacr.math.uwaterloo.ca/hac/
    """
    t = (e * d - 1)
    s = 0

    while True:
        quotient, remainder = divmod(t, 2)

        if remainder != 0:
            break

        s += 1
        t = quotient

    found = False

    while not found:
        i = 1
        a = random.randint(1,n-1)

        while i <= s and not found:
            c1 = pow(a, pow(2, i-1, n) * t, n)
            c2 = pow(a, pow(2, i, n) * t, n)

            found = c1 != 1 and c1 != (-1 % n) and c2 == 1

            i += 1

    p = fractions.gcd(c1-1, n)
    q = n // p

    return p, q

n 多因子

场景

当 n 由多个因子组成时

解法

多个因子时，我们根据欧拉函数求得对应的φ(n)即可

φ(x)=x∏i=1n(1−1/pi)

其中 pi 是 x 的所有质因数

选择明文攻击

场景

存在一个加密 Oracle，能够返回加密后的密文。求出对应的 e 和 n

解法

求解 e

当 e 较小时，可以通过 sage 的 bsgs 函数求得 e

1
2
3
4
5
6
7
8
9
# sage -python script.py
from sage.all import *
n = 
n = Zmod(n)
m = 
m = ZmodN(m)
c = 
c = ZmodN(c)
print(bsgs(m,c,(3, 2 ** 40)))

求解 n

分别加密、、、2、4、8、16…

我们可以得到：

c2=2emodn

c4=4emodn

c8=8emodn

那么：

c22≡c4modn

c23≡c8modn

所以有：

c22−c4=kn

c23−c8=tn

最后求得他们的公因子就是 n，使用的 Oracle 数据越多，公因子是 n 的概率越大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from pwm import *
import libnum
p = remote(ip,port)

p.recvuntil("m: ")
p.sendline("2")
c2 = int(p.recvline())

p.recvuntil("m: ")
p.sendline("4")
c4 = int(p.recvline())

p.recvuntil("m: ")
p.sendline("8")
c8 = int(p.recvline())

p.recvuntil("m: ")
p.sendline("16")
c16 = int(p.recvline())

p.recvuntil("m: ")
p.sendline("32")
c32 = int(p.recvline())

pn = pow(c2,2)-c4
qn = pow(c2,3)-c8
rn = pow(c2,4)-c16
sn = pow(c2,5)-c32

l = []
n = libnum.xgcd(pn,qn)[2]
l.append(n)
n = libnum.xgcd(pn,rn)[2]
l.append(n)
n = libnum.xgcd(pn,sn)[2]
l.append(n)
n = libnum.xgcd(qn,rn)[2]
l.append(n)
n = libnum.xgcd(qn,sn)[2]
l.append(n)
n = libnum.xgcd(rn,sn)[2]
l.append(n)
n = 0
for _ in l:
    if(l.count(_)>=3):
        n = _
if(n==0):
    print("nope")
    exit(0)
else:
    print("n:",n)

第三部分是基本的 Coppersmith 相关内容

依赖库：

  • gmpy2
  • pycrypto
  • pwntools
  • sage

引子

c=memodN, 当 |m|<N1/e 时，我们能很快求得 m 的值

当 |m|>N1/e 时，如果已知 m 的部分信息 m0，能不能恢复未知 x 的值，这就是 Corppersmith 要解决的问题

c=(m0+x)emodN

已知部分明文攻击

引理 1

假设 N 是一个未知因子组成的数，且存在一个因子 b≥Nβ,0<β≤1,f(x) 是一个一元δ阶多项式，且 c≥1，那么可以在 O(cδ5log9(N))复杂度内求解下列等式的所有的 x0

f(x)=0modb,|x0|≤cNβ2/δ

场景

设 m=m0+x0，其中 x0 是未知的，那么我们可以列出以下多项式

f(x)=(m0+x)e−cmodN,f(x0)=0

当 e 和 x0 很小的时候，Coppersmith 就能求出 x0 的值

解法

在这个场景中，我们知道 b=N,δ=e,β=1，设 c=1，此时 |x0|≤cNβ2/δ=N1/e，因此，为了求解 x0，我们需要知道原消息 m 至少 (1-1/e)*N.bit_length() 比特的信息

碰到的最常见的是已知明文高位攻击，但其实未知的部分在哪里都可以，只要是连贯的，就能构造对应的 f(x)进行求解

已知明文高位

1
2
3
4
5
6
7
8
9
10
e = 
c = 
n = 
kbits = # x 的未知 bit 数目
m0 =  #明文的高位信息
PR.<x> = PolynomialRing(Zmod(n))
f = (m0 + x)^e - c
f = f.monic()
x0 = f.small_roots(X=2^kbits,beta=1)[0] # 在 0 - 2^kbits 范围内求解小根，beta 为 1 和上述分析的 beta 一致，也就是对应 factor 为 N
print(x0)

已知明文低位

将构造的函数改为以下即可

1
f = ((m0 + ZmodN((pow(2,m0.nbits())))*x)^e) - c

当然, 如果是明文的中间部分 bit 未知，也是相同的去修改对应的多项式 f(x)即可，具体题目见https://cryptohack.org/challenges/rsa/ 中的 Null or Never 题目（Coppersmith 是该题的一种解法）

已知部分 p 攻击

场景

已知 p=p0+x, 且 |x|<N1/4 时，也就是知道 p 的大约一半 bits 信息时，可以得到对应的 x，从而对 N 进行分解

解法

此时根据 p=p0+x0 我们知道 p0=x0modp，所以可以列出多项式，f(x)=p0−xmodp，f(x0)=0modp

对应到引理中，显然 b=p，由于在 RSA 中，和 p 和 q 经常为同比特的素数，所以设置，beta=0.4，0.3 等都可

已知 p 高位

1
2
3
4
5
6
7
8
n = 
p0 = # 已知的 p 的高位
kbits = 
PR.<x> = PolynomialRing(Zmod(n))
f = x + p0
f = f.monic()
x0 = f.small_roots(X=2^kbits, beta=0.3)[0] # beta=0.3 表明存在 factor 大于 n ^0.3
print(x0 + p0)

已知 p 低位

同样的，已知 p 低位或者中间部分未知，修改对应的 f(x)的表达式即可，例如已知 p 低位，则

1
2
ZmodN=Zmod(n)
f(x) = x*ZmodN(pow(2,p0.nbits()))+p0

部分私钥暴露攻击

场景

当已知私钥的部分 bit 信息，私钥 d=d0+x，d0 的 bit 数目约为 d 的 1/4 时，可以恢复私钥 d

解法

根据论文《An Attack on RSA Given a Small Fraction of the Private Key Bits》

假设私钥 d 的 bit 数目为 kbits, 且已知的是私钥的低位

那么我们可以知道 d0=dmod2kbits

所以有 ed0=1+k(N−s+1)mod2kbits,(s=p+q)

所以我们可以通过解 ed0x−kx(N−x+1)=xmod2kbits 得到可能的 smod2kbits 的值，继续通过求解 p2−sp+N=0mod2kbits，就能得到 pmod2kbits 的值了，进而把问题转换为已知部分 p 攻击。下面这个日本大哥的脚本是把 1、2 两步结合起来列式了，所以只求一个方程解出了部分 p

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def partial_p(p0, kbits, n):
    PR.<x> = PolynomialRing(Zmod(n))
    nbits = n.nbits()

    f = 2^kbits*x + p0
    f = f.monic()
    roots = f.small_roots(X=2^(nbits//2-kbits), beta=0.3)  # find root < 2^(nbits//2-kbits) with factor >= n^0.3，在实际使用脚本的时候可以自己手动改 nbits 等参数，理解了原理再看脚本就很清楚明了了
    if roots:
        x0 = roots[0]
        p = gcd(2^kbits*x0 + p0, n)
        return ZZ(p)

def find_p(d0, kbits, e, n):
    X = var('X')

    for k in xrange(1, e+1):
        results = solve_mod([e*d0*X - k*X*(n-X+1) + k*n == X], 2^kbits)
        for x in results:
            p0 = ZZ(x[0])
            p = partial_p(p0, kbits, n)
            if p:
                return p


if __name__ == '__main__':
    n =
    e = 
    d0 = 
		kbits = # 未知的 d 的 bits 数目
    p = find_p(d0, kbits, e, n)
    print("found p: %d" % p)
    q = n//p
    print(inverse_mod(e, (p-1)*(q-1)))

如果将 1、2 两步分开列式，则修改函数 find_p 如下

1
2
3
4
5
6
7
8
9
10
11
12
13
def find_p(d0, kbits, e, n):
    X = var('X')
    for k in range(1, e+1):
        results = solve_mod([e*d0*X - k*X*(n-X+1)== X], 2^kbits)
        for x in results:
            s = ZZ(x[0])
            pvar = var('p')
            p_results = solve_mod([pvar*pvar-s*pvar+n==0],2^kbits)
            for p0 in p_results:
                p0 = ZZ(p0[0])
                p = partial_p(p0, kbits, n)
                if p:
                    return p

但是速度上好像慢一些。

同样的已知 d 高位等也可以进行求解，例如已知 d 高位，那么第一步解出来的其实是可能的 p 的低位，所以在解部分 p 时，修改 f = (2^kbits)*x + p0 即可

例题：2020 天翼杯 hardRSA

题目脚本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# chall.py
# flag{6809781d08e120627e623dcdafe26b8a}
p = getPrime(510)
q = getPrime(510)
r = getPrime(510)
e = 7
m = bytes_to_long(os.urandom(30) + flag)
n = p * q * r
d = invert(e, (p - 1) * (q - 1) * (r - 1))
c = pow(m, e, n)
print(n // p)
print(p)
print(c)
print(hex(d % (1 << 540)))

从题目看也是 Coppersmith partial d 的情况，只是这里由于 n 由、、p、q、r 三个素数组成，因此需要我们重新推导同余方程

已知：kbits=540、p、qr、d0 的值，d0=dmod2kbits

推导如下：
(1)ed0=1+k(p−1)(q−1)(r−1) =1+k(pq−p−q+1)(r−1) =1+k(pqr−pr−qr−1−pq+p+q+r) =1+k(N−p(r+q)+s−qr−1) =1+k(N−p(r+q)+(r+q)+p−qr−1) =1+k(N−ps+s+p−qr−1) =1+k(p−1)(qr−s+1)mod2kbits,(s=q+r)通过上式可以求得所有的 smod2kbits 的值，同时我们知道(2)q2−sq+qr=0mod2kbits 联立公式 1×q 和公式 2×k(p−1)，可以得到公式

(3)ed0q=q+kq(p−1)(qr−s+1)

(4)k(p−1)qr=kq(p−1)(s−q)

相加得到：

ed0q+k(p−1)qr=q+kq(p−1)(qr−q+1)

即：

ed0q+k(p−1)qr−k(p−1)q(qr−q+1)=qmod2kbits

解上述同余方程，即可得到 qmod2kbits

由于 kbits=540，而 q 只有 510bits，所以解出来的就是可能的 q 的值，再通过 qr 过滤即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def find_q(d0, kbits, e, qr, p):
    X = var('X')
    for k in range(1, e + 1):
        temp = k*(p-1)
        results = solve_mod([e*d0*X+temp*qr-temp*X*(qr-X+1)==X], 2 ^ kbits)
        for x in results:
            q = ZZ(x[0])
            if qr % q == 0:
                return q
    return None


if __name__ == '__main__':
    qr = 6857671284539062742975668483013695756136974308830302383869017675211748459038460434623218652374536550644287079851235538790745857383008797698872874798021995947967308637270510423795384863442755166813716746318469915880844736019524077541319597047087620854791342900521099848683663304636436936596021386279685708537
    p = 2141698433991046082370939321691850154692026423424010392532982575546199921995522418737105878977898158159119041866620684371362271661642476751663585379591337
    c = 4329606906986929520922207896899782825966852252045645553852666134465727605375552409314262439896695961792039946511877813768609658516837096110397826574615865145364406310497152725490038135469839136190625952342503082553246584871237205558902774064100332461452316195663446307120094941991930964324406679011451626126064494215289724959537793057773764253924636259378833228904446486925068109314698993641720938647836132806653451109926428309922461595730642461604303078237048
    d0 = 0x8e6f66a517d9c8a610eb65dac5a613e72d47a29beaa5c77a9eb857e0db5d09eadf3a317776fdf27b0d85db0b6677afc8e0683d6dc2b4580281b6e99c3050f649213c37
    e = 7
    kbits = 540
    q = find_q(d0, kbits, e, qr, p)
    print(q)
    # q = 2505948797318027758820680066583904581437202552654881626817593379353882875609223855015707273771918291251411562855290697544161987271016184806489110771554269

short padding attack

场景

Short padding attack 经常和 相关消息攻击结合 (https://blog.ycdxsb.cn/2decc525.html#more) 使用

我们已知 c1=memodn，c2=(m+padding)emodn，但我们不知道具体的 padding 值是多少

解法

首先通过 short padding attack 求出padding 的值，然后再使用相关消息攻击求得消息 m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def short_pad_attack(c1, c2, e, n):
    PRxy.<x,y> = PolynomialRing(Zmod(n))
    PRx.<xn> = PolynomialRing(Zmod(n))
    PRZZ.<xz,yz> = PolynomialRing(Zmod(n))

    g1 = x^e - c1
    g2 = (x+y)^e - c2

    q1 = g1.change_ring(PRZZ)
    q2 = g2.change_ring(PRZZ)

    h = q2.resultant(q1)
    h = h.univariate_polynomial()
    h = h.change_ring(PRx).subs(y=xn)
    h = h.monic()

    kbits = n.nbits()//(2*e*e)
    diff = h.small_roots(X=2^kbits, beta=0.5)[0]  # find root < 2^kbits with factor >= n^0.5

    return diff
 
 
def related_message_attack(c1, c2, diff, e, n):
    PRx.<x> = PolynomialRing(Zmod(n))
    g1 = x^e - c1
    g2 = (x+diff)^e - c2

    def gcd(g1, g2):
        while g2:
            g1, g2 = g2, g1 % g2
        return g1.monic()

    return -gcd(g1, g2)[0]

第四部分是相关消息的内容

依赖库：

  • gmpy2
  • pycrypto
  • pwntools
  • sage

线性相关消息

场景

这是相关消息攻击最简单的一种形式，已知，c1=m1emodN,c2=(am1+b)emodN，m2=am1+b

解法

可以看到两次加密的消息 m1 和 m2 存在线性关系，当 e=3 时，根据推导(见《Low-Exponent RSA with Related Messages》)，可以得到以下关系

m1=bac2+2a3c1−b3c2−a3c1+2b3，因此可以根据已知的、、、c1、c2、a、b 轻松得到消息 m1（注意，这里的除法是求逆元的意思）

1
2
3
4
5
6
7
8
9
# python
from gmpy2 import invert
def getmessage(a, b, c1, c2, n):
    b3 = pow(b, 3, n)
    a3 = pow(a, 3, n)
    part1 = b * (c2 + 2 * c1 * a3 - b3) % n
    part2 = a * (c2 - c1 * a3 + 2 * b3) % n
    part2 = invert(part2, n)
    return part1 * part2 % n

进阶

下面是论文中的通用情况，即 c1=(a1m+b1)emodn，c2=(a2m+b2)emodn，不通过前面推公式的方法，只需要通过 gcd 即可求得对应的消息。由于式子(a1m+b1)e−c1modn 和(a2m+b2)e−c2modn 都必然存在公共的 x−m 的根，因此通过 gcd 求得 x−m，即可得到对应的消息 m，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# sage
def gcd(g1, g2):
    while g2:
        g1, g2 = g2, g1 % g2
    return g1.monic()
    
n = 
a1 = 
b1 = 
c1 = 
a2 = 
b2 = 
e = 3
c2 = PR.<x>= PolynomialRing(Zmod(n))
g1 = (a1*x+b1)^e-c1
g2 = (a2*x+b2)^e-c2
print(-gcd(g1, g2)[0])

多消息相关

场景

假设存在 k 个消息，它们有关系式 P0(x1,x2,…xk)=p(x1,x2,…xk)=0modN

并且有 Pi(xi)=xie−ci=0modN，需要求解这 k 个消息

解法

根据这 k+1 个等式，我们计算 Groebner 基 Groebner([P0,P1,…Pk])，可以得到结果[x1−m1,…xk−mk]，

也就求得了所有的 k 个消息

以下举例论文中比较特殊的线性相关消息，即 P0(x1,x2…xk)=x1+x2+…xk−w=0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# python
from Crypto.Util.number import getPrime, bytes_to_long
p = getPrime(512)
q = getPrime(512)
n = p * q
e = 3
m1 = bytes_to_long(b"flag{This_is_flag1}")
m2 = bytes_to_long(b"flag{This_is_flag2}")
m3 = m1+m2+10000
print(n)
print(pow(m1,e,n))
print(pow(m2,e,n))
print(pow(m3,e,n))
'''
108684504406001730978107355065522913091470167674222436489722232508562878942265531378563853986279259519842855383477949581415300994618557266600557629814170912555530200441331549267805294484355321505430150563949802485514426432450612355535035910835277447960752175362457165729276266536456917482476441605301749223673
11916677858912595626741303803048763073265062084232819699152039070779448603839943645221450568650559197753804295090892194306963679051905125
11916677858912595626741303803048763073265066091036090039985967549263766666260772390533720397506805484501981105835442312723743004564263781
95333422871300765013930430424390104586121138764086629711853351243347558333657355599432416841199469970564180649403376333107226365096683496
'''

解的脚本如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# sage
e = 3
cnt = 3
N=108684504406001730978107355065522913091470167674222436489722232508562878942265531378563853986279259519842855383477949581415300994618557266600557629814170912555530200441331549267805294484355321505430150563949802485514426432450612355535035910835277447960752175362457165729276266536456917482476441605301749223673
c1=11916677858912595626741303803048763073265062084232819699152039070779448603839943645221450568650559197753804295090892194306963679051905125
c2=11916677858912595626741303803048763073265066091036090039985967549263766666260772390533720397506805484501981105835442312723743004564263781
c3=95333422871300765013930430424390104586121138764086629711853351243347558333657355599432416841199469970564180649403376333107226365096683496
c = [c1,c2,c3]
PR = PolynomialRing(Zmod(N), 'x', cnt)
x = PR.gens()
F = []
for i in range(cnt):
    F.append(pow(x[i],e)-c[i])
F.append(x[0]+x[1]-x[2]+10000)
I = Ideal(F)
G= I.groebner_basis()
for b in G[:-1]:
    mi = ZZ(-b(0, 0, 0))
    print(bytes.fromhex(hex(mi)[2:]))
'''
b'flag{This_is_flag1}'
b'flag{This_is_flag2}'
'''

Hastad 攻击

场景

前面的两个相关消息攻击模数都是相同的，而在 Hasted 广播攻击中则不同

使用不同但互质的模数 n，相同的指数 e、加密 e 个明文得到 e 个密文，即 ci=(aix+bi)emodni,i=1,2…e

解法

通过这 e 个式子，我们有 e 个等式：，(aix+bi)e−ci≡0modni，i=1,2…e

由于这 e 个式子中，模数都是互质的，那么通过中国剩余定理，我们可以得到，P(x)≡0modM，M=∏i=1eni，而 P(x)又必然存在唯一解，并满足 LLL 算法约束，因此可以通过 sage 的small_roots函数解得，以下给出两个写法分别来自https://github.com/ValarDragon/CTF-Crypto/blob/master/RSA/hastads.sage 和 https://xz.aliyun.com/t/6813

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# sage
def linearPaddingHastads1(cArray, nArray, aArray, bArray, e=3, eps=1/8):
    """
    Performs Hastads attack on raw RSA with no padding.
    This is for RSA encryptions of the form: cArray[i] = pow(aArray[i]*msg + bArray[i],e,nArray[i])
    Where they are all encryptions of the same message.
    cArray = Ciphertext Array
    nArray = Modulus Array
    aArray = Array of 'slopes' for the linear padding
    bArray = Array of 'y-intercepts' for the linear padding
    e = public exponent
    """
    if(len(cArray) == len(nArray) == len(aArray) == len(bArray) == e):
        for i in range(e):
            cArray[i] = Integer(cArray[i])
            nArray[i] = Integer(nArray[i])
            aArray[i] = Integer(aArray[i])
            bArray[i] = Integer(bArray[i])
        TArray = [-1]*e
        for i in range(e):
            arrayToCRT = [0]*e
            arrayToCRT[i] = 1
            TArray[i] = crt(arrayToCRT, nArray)
        P.<x> = PolynomialRing(Zmod(prod(nArray)))
        gArray = [-1]*e
        for i in range(e):
            gArray[i] = TArray[i]*(pow(aArray[i]*x + bArray[i], e) - cArray[i])
        g = sum(gArray)
        g = g.monic()
        # Use Sage's inbuilt coppersmith method
        roots = g.small_roots(epsilon=eps)
        if(len(roots) == 0):
            print("No Solutions found")
            return -1
        return roots[0]

    else:
        print("CiphertextArray, ModulusArray, and the linear padding arrays need to be of the same length," +
              "and the same size as the public exponent")

def linearPaddingHastads2(cArray, nArray, aArray, bArray, e=3, eps=1/8):
    cnt = e
    PR = PolynomialRing(ZZ, 'x')
    x = PR.gen()
    Fs = []
    for i in range(cnt):
        f = PR((A[i]*x + B[i])**e - Cs[i])
        ff = f.change_ring(Zmod(Ns[i]))
        ff = ff.monic()
        f = ff.change_ring(ZZ)
        Fs.append(f)

    F = crt(Fs, Ns)
    M = reduce(lambda x, y: x * y, Ns)
    FF = F.change_ring(Zmod(M))
    m = FF.small_roots(epsilon=1/16)
    if m:
        return m[0]
    else:
        return None

SMUPE 问题

场景

在经历了模数相同的相关消息攻击，也看过了模数不同的 Hastad 攻击，但是我们的指数 e 始终是一致的，SMUPE 问题是论文《Solving Systems of Modular Equations in One Variable: How Many RSA-Encrypted Messages Does Eve Need to Know? 》中提出的，不仅模数不同，且指数 e 也不同，具体如下：

假如我们有 k 个式子，ci=(aix+bi)eimodni,i=1,2…k，此时如何求解未知的消息呢

解法

示例 1：以论文中为例，已有 4 个公钥 (e,N) 分别为(3,N1),(3,N2),(5,N3),(5,N4)，且有 ci=(aix+bi)eimodNi,i=1,2…4

由于阶次不同，无法直接进行 CRT，因此需要构造得到同阶次的式子进行 CRT。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Cs = [...]
PKs =  [(3,..), (3,..), (5,..), (5,..)]
cnt = 4
A = []
B = []
PR = PolynomialRing(ZZ, 'x')
x = PR.gen()

Fs = []
for i in range(cnt):
    f =  PR(( A[i]*x + B[i] )**PKs[i][0] - Cs[i] )
    ff = f.change_ring(Zmod(PKs[i][1]) )
    ff = ff.monic()
    f = ff.change_ring(ZZ)
    Fs.append(f)
F = crt([ Fs[0]**2, Fs[1]**2, x*Fs[2], x*Fs[3] ], [PKs[i][1] for i in range(cnt) ] )

M = reduce(lambda x, y: x * y, [ PKs[i][1] for i in range(cnt) ] )
FF = F.change_ring(Zmod(M) )
m = FF.small_roots(X=2**760, beta=7./8)[0]
print(m)

示例 2：

也是为了更加深入理解这个构造，在此示例中，e 分别为 2 和 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
c1 = 
c2 = 
a1 = 
a2 = 
b1 = 
b2 = 

Cs = [c1, c2]
A = [a1, a2]
B = [b1, b2]
cnt = 2
PKs = [(2,n1), (3,n2)]
PR = PolynomialRing(ZZ, 'x')
x = PR.gen()
Fs = []
for i in range(cnt):
    f =  PR(( A[i]*x + B[i] )**PKs[i][0] - Cs[i] )
    ff = f.change_ring(Zmod(PKs[i][1]) )
    ff = ff.monic()
    f = ff.change_ring(ZZ)
    Fs.append(f)
F = crt([ Fs[0]*x, Fs[1]], [PKs[i][1] for i in range(cnt) ] )

M = reduce(lambda x, y: x * y, [ PKs[i][1] for i in range(cnt) ] )
FF = F.change_ring(Zmod(M) )
m = FF.small_roots(epsilon=1.0/16)[0]
print(m)

PS：small_roots的参数需要根据实际情况进行调整

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Let `N` be the characteristic of the base ring this polynomial
  is defined over: ``N = self.base_ring().characteristic()``.
  This method returns small roots of this polynomial modulo some
  factor `b` of `N` with the constraint that `b >= N^\beta`.
  Small in this context means that if `x` is a root of `f`
  modulo `b` then `|x| < X`. This `X` is either provided by the
  user or the maximum `X` is chosen such that this algorithm
  terminates in polynomial time. If `X` is chosen automatically
  it is `X = ceil(1/2 N^{\beta^2/\delta - \epsilon})`.
  The algorithm may also return some roots which are larger than `X`.
  'This algorithm' in this context means Coppersmith's algorithm for finding
  small roots using the LLL algorithm. The implementation of this algorithm
  follows Alexander May's PhD thesis referenced below.
  INPUT:
  - ``X`` -- an absolute bound for the root (default: see above)
  - ``beta`` -- compute a root mod `b` where `b` is a factor of `N` and `b
    \ge N^\beta`. (Default: 1.0, so `b = N`.)
  - ``epsilon`` -- the parameter `\epsilon` described above. (Default: `\beta/8`)
  - ``**kwds`` -- passed through to method :meth:`Matrix_integer_dense.LLL()

绕过 Miller-Rabin 素性测试

题目要求在 2**600 到2**900范围内找到一个数，这个数不是质数，但可以通过 Miller-Rabin 素性测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def generate_basis(n):
    basis = [True] * n
    for i in range(3, int(n**0.5)+1, 2):
        if basis[i]:
            basis[i*i::2*i] = [False]*((n-i*i-1)//(2*i)+1)
    return [2] + [i for i in range(3, n, 2) if basis[i]]


def miller_rabin(n, b):
    """
    Miller Rabin test testing over all
    prime basis < b
    """
    basis = generate_basis(b)
    if n == 2 or n == 3:
        return True

    if n % 2 == 0:
        return False

    r, s = 0, n - 1
    while s % 2 == 0:
        r += 1
        s //= 2
    for b in basis:
        x = pow(b, s, n)
        if x == 1 or x == n - 1:
            continue
        for _ in range(r - 1):
            x = pow(x, 2, n)
            if x == n - 1:
                break
        else:
            return False
    return True
  
miller_rabin(p,64)

从虽然从参考资料中的论文给出了一些示例，但都不符合题目的限制，不过好在参考资料的 appendix A 里给了十分完整的示例，可以对着复现和验证

假设我们的伪素数 n=p1p2…ph，其中 pi 是不同的素数，使得 n 是基 a1,a2…at 下的伪素数，在本文中，h=3

论文中的方法是先找到一个 p1，然后生成 pi=ki(pi−1)+1，最后合成伪素数 n

找 p1 的步骤如下

Step1：求 Sa

image-20201009203311692

显然对于 miller_rabin(p,64) 而言，我们的 A 为 64 以下的所有质数，求 A 如下

1
2
3
4
5
6
7
8
9
10
def generate_basis(n):
    basis = [True] * n
    for i in range(3, int(n**0.5)+1, 2):
        if basis[i]:
            basis[i*i::2*i] = [False]*((n-i*i-1)//(2*i)+1)
    return [2] + [i for i in range(3, n, 2) if basis[i]]

A = generate_basis(64)
print('A:', A)
# [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61]

而我们要求的 Sa 集合，它要求，对于每个基 a，在3~(4*a-1) 范围内所有与 a 的Jacobi结果为 -1 的数字的集合，如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Sa = {}
print("Sa: ")
for a in A:
    Sa[a] = []
    for _ in range(3, 4*a-1, 2):
        if libnum.jacobi(a, _) == -1:
            Sa[a].append(_)
    print(a, Sa[a])
'''
Sa:
2 [3, 5]
3 [5, 7]
5 [3, 7, 13, 17]
7 [5, 11, 13, 15, 17, 23]
11 [3, 13, 15, 17, 21, 23, 27, 29, 31, 41]
13 [5, 7, 11, 15, 19, 21, 31, 33, 37, 41, 45, 47]
17 [3, 5, 7, 11, 23, 27, 29, 31, 37, 39, 41, 45, 57, 61, 63, 65]
19 [7, 11, 13, 21, 23, 29, 33, 35, 37, 39, 41, 43, 47, 53, 55, 63, 65, 69]
23 [3, 5, 17, 21, 27, 31, 33, 35, 37, 39, 45, 47, 53, 55, 57, 59, 61, 65, 71, 75, 87, 89]
29 [3, 11, 15, 17, 19, 21, 27, 31, 37, 39, 41, 43, 47, 55, 61, 69, 73, 75, 77, 79, 85, 89, 95, 97, 99, 101, 105, 113]
31 [7, 13, 17, 19, 21, 29, 35, 37, 39, 47, 51, 53, 57, 59, 61, 63, 65, 67, 71, 73, 77, 85, 87, 89, 95, 103, 105, 107, 111, 117]
37 [5, 13, 15, 17, 19, 23, 29, 31, 35, 39, 43, 45, 51, 55, 57, 59, 61, 69, 79, 87, 89, 91, 93, 97, 103, 105, 109, 113, 117, 119, 125, 129, 131, 133, 135, 143]
41 [3, 7, 11, 13, 15, 17, 19, 27, 29, 35, 47, 53, 55, 63, 65, 67, 69, 71, 75, 79, 85, 89, 93, 95, 97, 99, 101, 109, 111, 117, 129, 135, 137, 145, 147, 149, 151, 153, 157, 161]
43 [5, 11, 15, 23, 29, 31, 33, 35, 37, 45, 47, 59, 61, 65, 67, 69, 73, 77, 79, 83, 85, 87, 89, 93, 95, 99, 103, 105, 107, 111, 113, 125, 127, 135, 137, 139, 141, 143, 149, 157, 161, 167]
47 [3, 5, 7, 13, 27, 29, 33, 41, 45, 51, 55, 57, 59, 63, 69, 71, 73, 75, 77, 79, 83, 85, 93, 95, 103, 105, 109, 111, 113, 115, 117, 119, 125, 129, 131, 133, 137, 143, 147, 155, 159, 161, 175, 181, 183, 185]
53 [3, 5, 19, 21, 23, 27, 31, 33, 35, 39, 41, 45, 51, 55, 61, 65, 67, 71, 73, 75, 79, 83, 85, 87, 101, 103, 109, 111, 125, 127, 129, 133, 137, 139, 141, 145, 147, 151, 157, 161, 167, 171, 173, 177, 179, 181, 185, 189, 191, 193, 207, 209]
59 [3, 7, 13, 15, 19, 27, 33, 35, 37, 51, 61, 63, 65, 69, 71, 73, 75, 77, 79, 87, 89, 93, 95, 97, 101, 107, 109, 113, 117, 119, 123, 127, 129, 135, 139, 141, 143, 147, 149, 157, 159, 161, 163, 165, 167, 171, 173, 175, 185, 199, 201, 203, 209, 217, 221, 223, 229, 233]
61 [7, 11, 17, 21, 23, 29, 31, 33, 35, 37, 43, 51, 53, 55, 59, 63, 67, 69, 71, 79, 85, 87, 89, 91, 93, 99, 101, 105, 111, 115, 129, 133, 139, 143, 145, 151, 153, 155, 157, 159, 165, 173, 175, 177, 181, 185, 189, 191, 193, 201, 207, 209, 211, 213, 215, 221, 223, 227, 233, 237]
'''

Step2：求 Sb

image-20201009204918929

在求 Sb 前，我们需要先指定 ki 的值(只要是质数就行)，这里我们指定、k2=701、k3=257

我们可以看到 Sb 其实就是取了一个 ki−1(Sa+ki−1)的交集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
print("Sb:")
Sb = {}
for a in A:
    result = []
    for b in Sa[a]:
        if((k2*(b-1)+1) % (4*a) in Sa[a] and (k3*(b-1)+1) % (4*a) in Sa[a]):
            result.append(b)
        Sb[a]=result
    print(a,Sb[a])
'''
Sb:
2 [3, 5]
3 [7]
5 [7, 17]
7 [11, 13, 15]
11 [17, 23, 41]
13 [21, 47]
17 [29, 63]
19 [29, 39, 47, 55]
23 [5, 31, 47, 59, 61]
29 [21, 41, 55, 79, 99, 113]
31 [17, 19, 37, 39, 63, 95]
37 [13, 17, 19, 23, 29, 31, 45, 61, 69, 87, 91, 93, 97, 103, 105, 119, 135, 143]
41 [17, 35, 63, 67, 69, 99, 117, 145, 149, 151]
43 [31, 33, 35, 37, 47, 61, 85, 87, 89, 105, 143]
47 [41, 45, 59, 69, 71, 79, 95, 103, 147, 161, 181]
53 [27, 61, 65, 67, 75, 83, 85, 87, 133, 167, 171, 173, 181, 189, 191, 193]
59 [33, 51, 69, 79, 95, 97, 113, 119, 127, 141, 157, 159, 165, 185]
61 [7, 17, 23, 55, 59, 69, 105, 111, 129, 139, 145, 177, 181, 191, 227, 233]
'''

Step3 ：CRT 求 p1

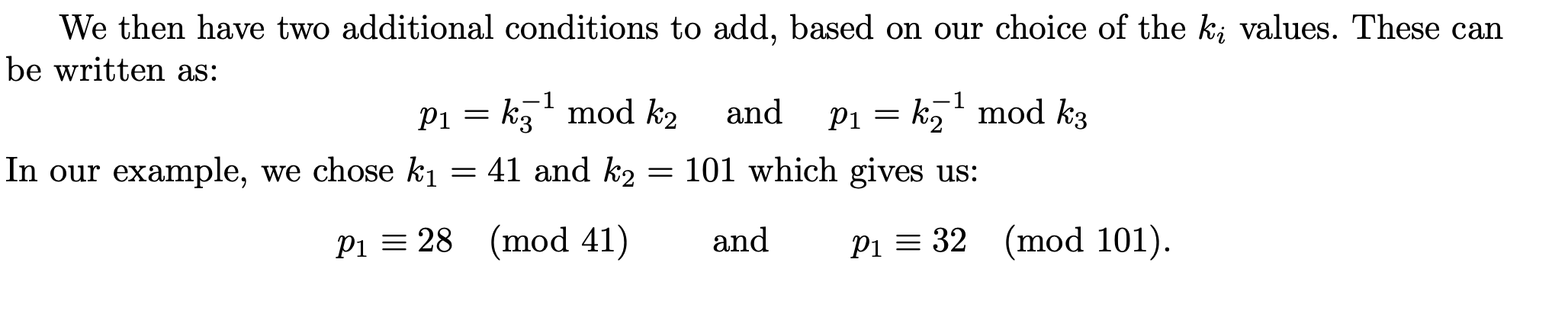
image-20201009205950893

最后从每个基的 Sb 集合中选择一个，进行 CRT 求出 p1

由于是随机选取，所以 CRT 未必满足条件，因此要多次 random 选出能成功 CRT 的序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
p1 = - inverse(k3, k2) % k2
p2 = - inverse(k2, k3) % k3
print(p1, p2)
print(isPrime(k2), isPrime(k3))
for i in range(0, 100000):
    try:
        crt_A = []
        crt_B = []
        for a in A:
            crt_A.append(random.choice(Sb[a]))
            crt_B.append(4*a)
        crt_A.append(p1)
        crt_A.append(p2)
        crt_B.append(k2)
        crt_B.append(k3)
        print(crt(crt_A, crt_B))
        print(crt_A)
        print(crt_B)
        break
    except:
        continue

p1 = crt(crt_A, crt_B)

然后求一下 p1 的模数，根据 pi=ki(p1−1)+1 求出其余的数，稍微调整一下大小到 600bits-900bits 之间即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
d = {}
for n in crt_B:
    k = factorize(n)
    for key in k.keys():
        if(key in d.keys()):
            if(d[key] < k[key]):
                d[key] = k[key]
        else:
            d[key] = k[key]
mod_number = 1
for key in d.keys():
    mod_number *= pow(key, d[key])
print('mod:', mod_number)
for _ in range(100000):
    if(_ % 10000 == 0):
        print(_)
    p1 = p1+mod_number*_*pow(2,100)
    p2 = k2*(p1-1)+1
    p3 = k3*(p1-1)+1
    if(isPrime(p1) and isPrime(p2) and isPrime(p3)):
        n = p1*p2*p3
        if(miller_rabin(n, 64)):
            print(p1, p2, p3)
            print(n)
            print(miller_rabin(n, 64))
            break

完整 exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
# https://eprint.iacr.org/2018/749.pdf
import libnum
from libnum.factorize import factorize
from sage.all import *
import random
from Crypto.Util.number import inverse, isPrime

def generate_basis(n):
    basis = [True] * n
    for i in range(3, int(n**0.5)+1, 2):
        if basis[i]:
            basis[i*i::2*i] = [False]*((n-i*i-1)//(2*i)+1)
    return [2] + [i for i in range(3, n, 2) if basis[i]]


def miller_rabin(n, b):
    """
    Miller Rabin test testing over all
    prime basis < b
    """
    basis = generate_basis(b)
    if n == 2 or n == 3:
        return True

    if n % 2 == 0:
        return False

    r, s = 0, n - 1
    while s % 2 == 0:
        r += 1
        s //= 2
    for b in basis:
        x = pow(b, s, n)
        if x == 1 or x == n - 1:
            continue
        for _ in range(r - 1):
            x = pow(x, 2, n)
            if x == n - 1:
                break
        else:
            return False
    return True


A = generate_basis(64)
print('A:', A)
Sa = {}
print("Sa: ")
for a in A:
    Sa[a] = []
    for _ in range(3, 4*a-1, 2):
        if libnum.jacobi(a, _) == -1:
            Sa[a].append(_)
    print(a, Sa[a])

k2 = 701
k3 = 257

print("Sb:")
Sb = {}
for a in A:
    result = []
    for b in Sa[a]:
        if((k2*(b-1)+1) % (4*a) in Sa[a] and (k3*(b-1)+1) % (4*a) in Sa[a]):
            result.append(b)
        Sb[a]=result
    print(a,Sb[a])
p1 = - inverse(k3, k2) % k2
p2 = - inverse(k2, k3) % k3
print(p1, p2)
print(isPrime(k2), isPrime(k3))
for i in range(0, 100000):
    try:
        crt_A = []
        crt_B = []
        for a in A:
            crt_A.append(random.choice(Sb[a]))
            crt_B.append(4*a)
        crt_A.append(p1)
        crt_A.append(p2)
        crt_B.append(k2)
        crt_B.append(k3)
        print(crt(crt_A, crt_B))
        print(crt_A)
        print(crt_B)
        break
    except:
        continue

p1 = crt(crt_A, crt_B)
d = {}
for n in crt_B:
    k = factorize(n)
    for key in k.keys():
        if(key in d.keys()):
            if(d[key] < k[key]):
                d[key] = k[key]
        else:
            d[key] = k[key]
mod_number = 1
for key in d.keys():
    mod_number *= pow(key, d[key])
print('mod:', mod_number)
for _ in range(100000):
    if(_ % 10000 == 0):
        print(_)
    p1 = p1+mod_number*_*pow(2,100)
    p2 = k2*(p1-1)+1
    p3 = k3*(p1-1)+1
    if(isPrime(p1) and isPrime(p2) and isPrime(p3)):
        n = p1*p2*p3
        if(miller_rabin(n, 64)):
            print(p1, p2, p3)
            print(n)
            print(miller_rabin(n, 64))
            break

'''
A: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61]
Sa:
2 [3, 5]
3 [5, 7]
5 [3, 7, 13, 17]
7 [5, 11, 13, 15, 17, 23]
11 [3, 13, 15, 17, 21, 23, 27, 29, 31, 41]
13 [5, 7, 11, 15, 19, 21, 31, 33, 37, 41, 45, 47]
17 [3, 5, 7, 11, 23, 27, 29, 31, 37, 39, 41, 45, 57, 61, 63, 65]
19 [7, 11, 13, 21, 23, 29, 33, 35, 37, 39, 41, 43, 47, 53, 55, 63, 65, 69]
23 [3, 5, 17, 21, 27, 31, 33, 35, 37, 39, 45, 47, 53, 55, 57, 59, 61, 65, 71, 75, 87, 89]
29 [3, 11, 15, 17, 19, 21, 27, 31, 37, 39, 41, 43, 47, 55, 61, 69, 73, 75, 77, 79, 85, 89, 95, 97, 99, 101, 105, 113]
31 [7, 13, 17, 19, 21, 29, 35, 37, 39, 47, 51, 53, 57, 59, 61, 63, 65, 67, 71, 73, 77, 85, 87, 89, 95, 103, 105, 107, 111, 117]
37 [5, 13, 15, 17, 19, 23, 29, 31, 35, 39, 43, 45, 51, 55, 57, 59, 61, 69, 79, 87, 89, 91, 93, 97, 103, 105, 109, 113, 117, 119, 125, 129, 131, 133, 135, 143]
41 [3, 7, 11, 13, 15, 17, 19, 27, 29, 35, 47, 53, 55, 63, 65, 67, 69, 71, 75, 79, 85, 89, 93, 95, 97, 99, 101, 109, 111, 117, 129, 135, 137, 145, 147, 149, 151, 153, 157, 161]
43 [5, 11, 15, 23, 29, 31, 33, 35, 37, 45, 47, 59, 61, 65, 67, 69, 73, 77, 79, 83, 85, 87, 89, 93, 95, 99, 103, 105, 107, 111, 113, 125, 127, 135, 137, 139, 141, 143, 149, 157, 161, 167]
47 [3, 5, 7, 13, 27, 29, 33, 41, 45, 51, 55, 57, 59, 63, 69, 71, 73, 75, 77, 79, 83, 85, 93, 95, 103, 105, 109, 111, 113, 115, 117, 119, 125, 129, 131, 133, 137, 143, 147, 155, 159, 161, 175, 181, 183, 185]
53 [3, 5, 19, 21, 23, 27, 31, 33, 35, 39, 41, 45, 51, 55, 61, 65, 67, 71, 73, 75, 79, 83, 85, 87, 101, 103, 109, 111, 125, 127, 129, 133, 137, 139, 141, 145, 147, 151, 157, 161, 167, 171, 173, 177, 179, 181, 185, 189, 191, 193, 207, 209]
59 [3, 7, 13, 15, 19, 27, 33, 35, 37, 51, 61, 63, 65, 69, 71, 73, 75, 77, 79, 87, 89, 93, 95, 97, 101, 107, 109, 113, 117, 119, 123, 127, 129, 135, 139, 141, 143, 147, 149, 157, 159, 161, 163, 165, 167, 171, 173, 175, 185, 199, 201, 203, 209, 217, 221, 223, 229, 233]
61 [7, 11, 17, 21, 23, 29, 31, 33, 35, 37, 43, 51, 53, 55, 59, 63, 67, 69, 71, 79, 85, 87, 89, 91, 93, 99, 101, 105, 111, 115, 129, 133, 139, 143, 145, 151, 153, 155, 157, 159, 165, 173, 175, 177, 181, 185, 189, 191, 193, 201, 207, 209, 211, 213, 215, 221, 223, 227, 233, 237]
Sb:
2 [3, 5]
3 [7]
5 [7, 17]
7 [11, 13, 15]
11 [17, 23, 41]
13 [21, 47]
17 [29, 63]
19 [29, 39, 47, 55]
23 [5, 31, 47, 59, 61]
29 [21, 41, 55, 79, 99, 113]
31 [17, 19, 37, 39, 63, 95]
37 [13, 17, 19, 23, 29, 31, 45, 61, 69, 87, 91, 93, 97, 103, 105, 119, 135, 143]
41 [17, 35, 63, 67, 69, 99, 117, 145, 149, 151]
43 [31, 33, 35, 37, 47, 61, 85, 87, 89, 105, 143]
47 [41, 45, 59, 69, 71, 79, 95, 103, 147, 161, 181]
53 [27, 61, 65, 67, 75, 83, 85, 87, 133, 167, 171, 173, 181, 189, 191, 193]
59 [33, 51, 69, 79, 95, 97, 113, 119, 127, 141, 157, 159, 165, 185]
61 [7, 17, 23, 55, 59, 69, 105, 111, 129, 139, 145, 177, 181, 191, 227, 233]
30 246
1 1
61933256682223994457337248907
[3, 7, 7, 11, 23, 47, 63, 39, 31, 79, 39, 103, 151, 31, 59, 87, 127, 111, 30, 246]
[8, 12, 20, 28, 44, 52, 68, 76, 92, 116, 124, 148, 164, 172, 188, 212, 236, 244, 701, 257]
mod: 84521291682266726685731893560
0
434373326067214608775878317645775351280862168574601991542247144587 304495701573117440751890700669688521247884380170795996071115248354787 111633944799274154455400727634964265279181577323672711826357516158603
14765242572717201537350357000818561932573315288396435774266341361498670863676541981221739664014401028330587564384701242669740856196369695370339038363927740181650866851457768843113763288312682772243647307
True
'''

相关

费马分解

image-20221101114309032

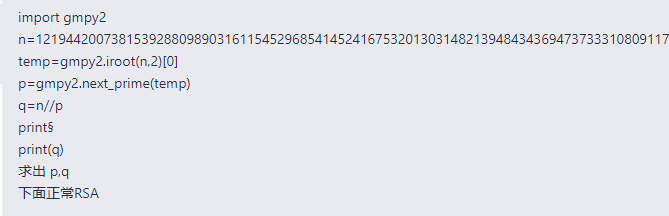
image-20221101114329560

Rabin 加密

Rabin 密码系统是第一个非对称密码系统，由Michael Oser Rabin 于 1979 年在论文 *Digitalized Signatures and Public-Key Functions as Intractable as Factorization* 中发表。可以证明从密文中恢复明文与分解一样困难，它的安全性来源于大整数的因子分解。优点：

  1. Rabin 函数的每个输出都可以由四个可能的输入中的任何一个生成
  2. 如果每个输出都是密文，则解密时需要额外的复杂性来识别四个可能的输入中的哪一个是真正的明文

image-20220524231559461

image-20220524231606916

(71 条消息) CTFshow- 卷网杯 -crypto- 真·简单·不卷·现代密码签到（复现）_这就是强者的世界么的博客 -CSDN 博客

(71 条消息) 卷王杯 - 部分 Crypto-wp_mxx307 的博客 -CSDN 博客

kali 工具

readelf ：

查看 elf 信息

objdump：

查看 elf 反汇编信息

带你认识 Linux 中的 ELF 文件 | w3c 笔记 (w3cschool.cn)

≡